象差的概念

上篇我们介绍过薄透镜物象之间的关系，是物体发出的光束经薄透镜成理想象的关系。在确定这些关系时，总是认为：物空间里一物点发出的光束通过透镜后在象空间成一完善的象点。由此形成的象点叫理想象点。由理想象点构成的与原物形状相似，颜色相同的象，称之为理想象。

实际上对单一薄透镜来说，只有在单色光和近轴光线成象时才是理想象。公式(2—5)、(2—6)和图2—9所示作图法均为薄透镜成理想象时所遵守的规律。

实际的光学系统一般都不是在单色近轴光情况下成象，而是在多色宽光束下成象，这种成象与理想成象之间有很大的偏离。实际成象与理想成象之间的偏离就是光学系统的象差。象差的存在影响象的清晰度和物象之间的相似性。

从象差产生的原因和影响成象质量的性质来看，可以把象差分为两类：一类是单色光成象时的象差，简称单色象差，它有球差、慧差、象散、场曲和畸变五种。另一类是多色光成象时，由于介质折射率随光的波长不同而变化所引起的象差，称为色象差。它有轴向色差和垂轴色差两种。

除铀向色差和球差是属于轴上物点的象差外，其余的都属于额外物点的象差。在七种象差中，只有畸变不影响象的清晰度，仅破坏物象之间的相似性。其它的六种象差，都在一定程度上破坏象的清晰度。

(1)球差

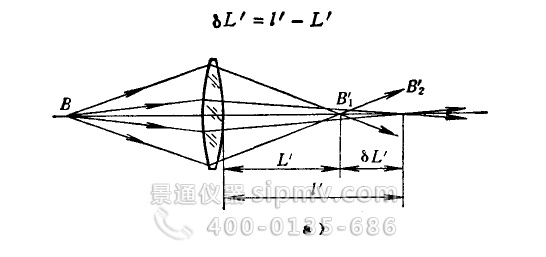
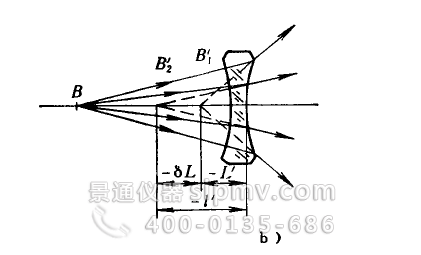
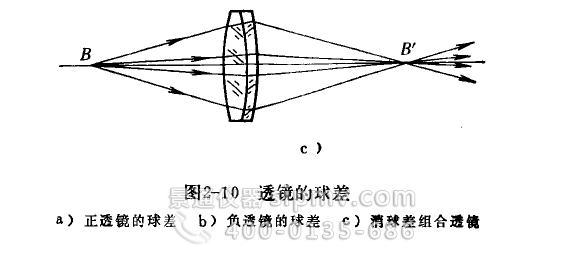
球差是由于光轴上物点用单色宽光束通过透镜成象时，不同入射高度的光线折射后交光铀于不问点所产生的，见图2—10a)、b)。光轴上物点B发出的单色光束，经透镜边缘的光线折射后交光铀于B'1点，截距Θ为L’；而靠近光轴的光线折射后交光轴子B'2点，截距为l’。如果我们把观察屏放在B'1、B'2点之间的任何位置，所看到的都不是一个理想的象点，而是一个弥散的光斑，与理想象点比较，有很大的偏离。一般定义上述截距之差(l’—L’)为透镜的球差，用符号δL'表示，即

TIPS: Θ 此处截距实际上指的是象方截距，它是从透镜系统最后一个折射球面与光轴交点算起的象距。

在光学系统中适当地改变透镜参数和组合可以校正球差，如图2—10 c)所示，这样的光学系统称为消球差系统。

(2)慧差

慧差的产生是由于轴外物点A发出的单色宽光束对光轴不对称，经过光学系统后在理想象平面上形成一个锥形散射斑。它的形状象拖着尾巴的彗星，因此这种象差称为慧差，见团2—11。

根据象差理论可以证明，与光轴垂直的小物面上各物点发出的光线，通过一个消球差的光学系统成象，同时物象之间的关系又满足下列的正弦条件：

nY sinU = n'Y'sinU'    (2-8)

则这个消球差的系统也是消慧差的光学系统。
式中 

n、n' - 物方、象方的折射率；
Y、Y' - 近轴物点的物高与象高；
U、U' - 物方斜角、象方斜角。

光轴上校正了球差又满足正弦条件的一对共轭点(物、象对应点)，称为齐明点或不晕点。金相显微镜的油浸物镜头两片透镜就是两次应用齐明点的原理设计的，所以该油浸
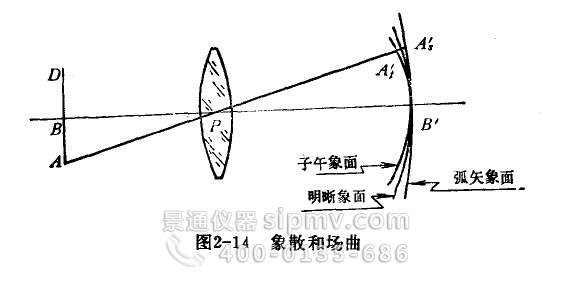
物镜在高倍放大条件下仍能保证有良好的成象质量，见图2—12。S为金相试样表面,它上面有一层折射率与第一个半球透镜很近似的油层，C1为第一个半球透镜的球心，S和S1为第一半球透镜的不晕点，S经第一个半球透镜成一完善象S1。正弯月透镜的第一个折射球面的曲率中心C2位于虚象S1处。因此，光线进入正弯月透镜的第一个折射面时，不会改变方向。选择正弯月透镜的第二个折射面的曲率（C3为其曲率中心），使S1距C3有合适的距离，则正弯月透镜第二折射面又一次不晕地将S1成此象于S2。这就是不晕点在金相显微物镜中应用的例子。

（3）象散和场曲

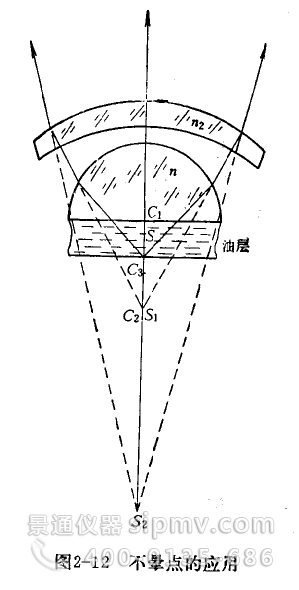
象散的产生，是由于远离光轴的倾斜细光束投射到透镜时，透镜对不同方向的光线有不同的会聚能力所引起的。从图2—13中可以看出：由远离光轴BPB'的物点A发出的光束对透镜来说不是正圆锥形的，此时出射光束不再存在对称轴线，而只存在一个对称面。这个对称面就是通过光轴BB'和入射光束的中心光线(主光线)AP所决定的平面(子午面)。通过主光线与子午面垂直的平面叫弧矢面。透镜对这两个截面内的光线有不同的会聚能力，在子午面内光线焦点为A't，再弧矢面内光线焦点为A's，和子午面平行的截面内光线会聚成与子午面垂直的子午焦线Ft A't F't ； 和弧矢面平行的截面内光线会聚成与弧矢面垂直的弧矢焦线Fs A's F's；而在两焦线间出现一系列的椭圆和一个圆（常称为明晰圆）。

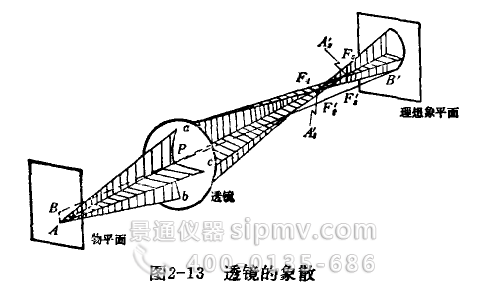
如果考虑与光轴正交的物平面上所有物点以细光束成象情况，与这些物点对应的A'1、A's的轨迹是两个绕光轴旋转的曲面，分别称为子午象面和弧矢象面，而明晰圆的轨迹称为明晰象面，见图2—14所示。这三个面在光轴上彼此相切。一般说来，明晰象面不是平面，而是一个曲面，这种象差叫做象面弯曲，简称场曲。子午象面与弧矢象面不重合，就叫做象散。若子午象面、弧矢象面和明晰象面三者重合为一个平面，则象散和场曲就完全校正了。在一定的象方视场内校正了象面弯曲和象散的物镜叫平场物镜。国产VM2200M型立式金相显微镜和VM5000M大型金相显微镜中的干燥系物镜都是平场消色差物镜。

（4）畸变

上面讨论的球差、慧差、象散和场曲均影响象的清晰度，而畸变则影响物、象之间的几何相似性。畸变是指在整个象面范围内由于各处的垂轴放大率不同而使象与原物在形状上失真。

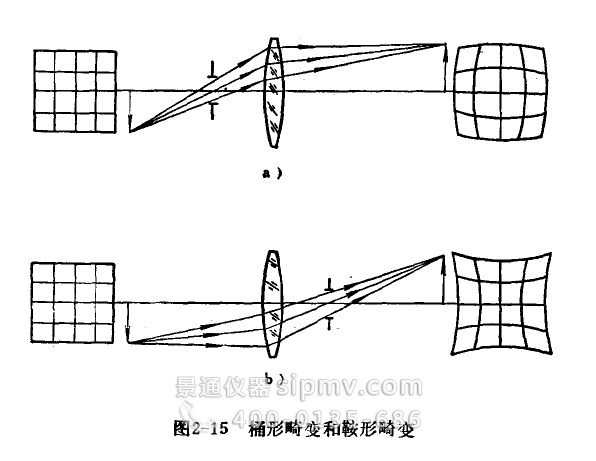
如果与光轴距离越远的地方垂轴放大率越小，结果方格网状的物将成一桶形，如图2—15a)所示，这种畸变叫桶形畸变或负畸变。如果与光轴距离越远的地方垂轴放大率越大，结果方格网状的物将成一鞍形，如图2—15b)所示，这种畸变叫鞍形畸变或正畸变。

畸变的存在除了象的相似性被破坏以外，对成象的清晰度无显著的影响。因此，只要眼睛看不出由于畸变而引起的变形，则这种象差对金相显微镜没有多大妨碍。

（5）色差

色差是由于玻璃对不同波长的单色光具有不同的折射率所引起的，因此，当物体发出白光时，以其中红光C(波长为6562.8埃)、黄光D(波长为5992.8埃)、蓝光F(波长为4861.3埃)为例，由于各色光线有不同的传播途径，结果使它们有不同的成象位置(见图2—16)，又有不同的成象高度(见图2—17)。这就是轴向色差和垂轴色差。

1)轴向色差

轴向色差(或称位置色差)是指各种色光的成象位置沿铀向之差。普通光学玻璃的透镜，对红光C的折射率较小，折射后交光轴于B'c点，离透镜较远，而对蓝光F的折射率较大，折射后交光袖于B'f点，离透镜较近，黄光D则在它们之间。通常用C、F两种波长光线的成象位置之差来表示轴向色差(用符号ΔL'cf表示)：

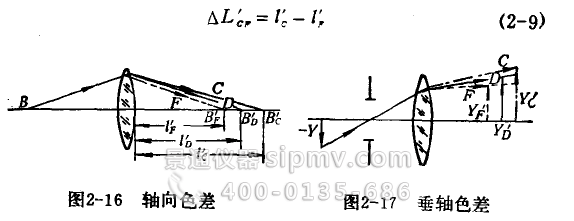
当一个光学系统的ΔL'cf > 0时，称为色差校正不足；反之，如ΔL'cf < 0，称为色差校正过头。从图2-16中容易看出，由于轴向色差的存在，使用白光成象时会出现有彩色的象。为了避免这种现象，金相显微镜的物镜都应时消轴向色差的，即ΔL'cf接近于零。

2）垂轴色差

垂轴色差（或称放大率色差）是指各种色光成象大小不一样。通常用C、F两种波长光线在同一象平面上的象高之差表示垂轴色差（用符号ΔL'cf表示），见图2-17，即

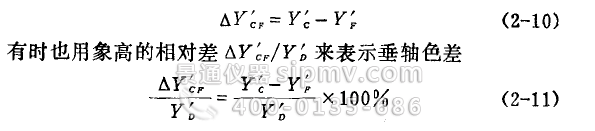
由于垂轴色差使物体用白光成象时在象的边缘出现彩色，所以视场较大的光学系统必须校正垂轴色差。金相显微镜目镜属于这种系统，故应较好地校正这种色差。从薄透镜组的消色差理论可以证明，用同种材料制成的、象方焦距分别为f'1、f'2，相距为d的两薄透镜（在空气中使用），当d、f'1和f'2之间满足下列关系时，就能消垂轴色差，即

惠更斯目镜和冉斯登目镜均属于消垂轴色差的薄透镜组。