前篇回顾：显微镜多少钱一台？

薄透镜的理想成象公式

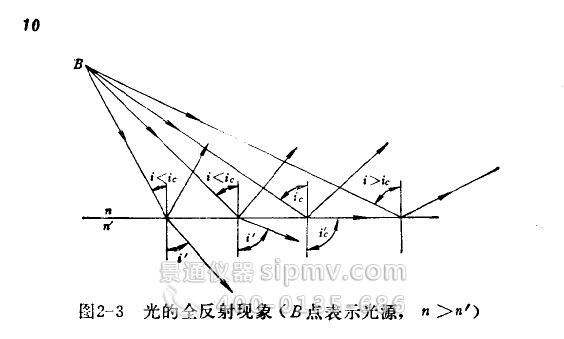
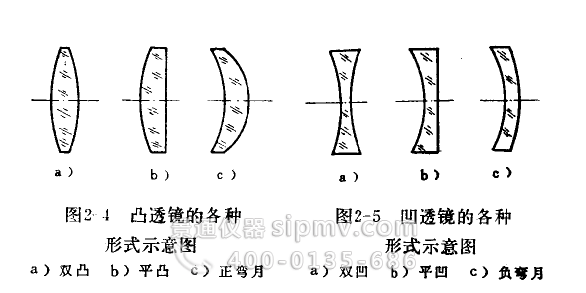
透镜是一切光学仪器的主要零件，它可以使光线会聚或发散，使物象放大或缩小。透镜的中央部分比边缘部分厚的叫凸透锐，见图2—4。中央部分比边缘部分薄的叫凹透镜，见图2—5。透镜的表面通常都做成球面(其中之一可以是平面)，但也有采用其它非球面形状的，例如国产立式、大型卧式金相显微镜中光源和孔径光栏之间的聚光镜就使用了双曲面透镜。

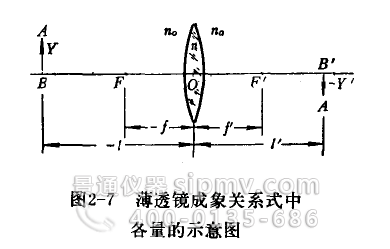
透镜两球面曲率中心的连线叫光抽。厚度相对球面曲率半径来说非常小的透镜称作薄远镜。薄透镜与光轴的交点O(见图2—7)叫薄透镜的光心。实验和理论可以证明：只要薄透镜放在同一介质中使用，通过光心的光线可以看作是一直穿过而不偏折的。

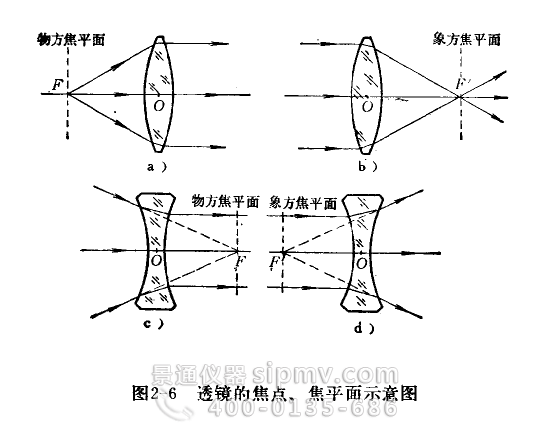
在透镜的光轴上总可以找到一点F，如果把点光源放在该点上，则通过透镜后的光线会变成平行于光轴的光线射出，光轴上的这个F点，叫透镜的物方焦点。F点到薄透镜光心O的距离叫物方焦距，通常用符号 f 表示。如果入射光是平行于透镜光轴的平行光线，则通过透镜后的光线会被会聚到一个 F’ 点上，这个点叫透镜的象方焦点，F’ 到薄透镜光心 O 的距离叫象方焦距，通常用符号 f’ 表示。通过物方焦点F且垂直于光轴的平面叫物方焦平面；通过象方焦点 F’ 且垂直于光轴的平面叫象方焦平面。图2—6分别画出了透镜放在光疏介质中使用时物方焦点、物方焦平面，象方焦点、象方熊平面之示意图。  

从几何光学的理论和实践可以证明，对放在同一介质中使用的薄透镜，在单色近轴光线成象条件下，物象位置关系以及垂轴放大率分别为：

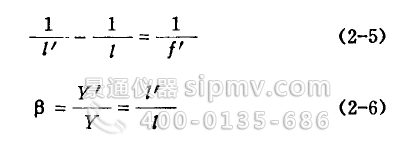
式中各量的正值在图2—7中均有标明，其中

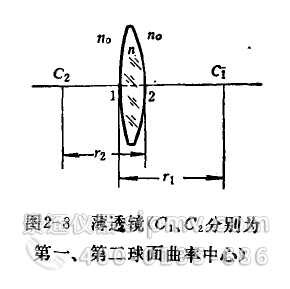
• f ——物距，从光心到轴上物点的距离[规定以光心为计算起点，从左向右为正值，从石向左为负值)；
• l' ——象距，从光心到轴上象点的距离(符号规定向物距)；
• Y ——物高(轴上方物高为正，轴下方物高为负)；
• Y’ ——象高(符导规定同物高)；
• β 一垂轴放大率，β的意义为象高Y‘与物高Y之比；
• f ——物方焦距(从光心到物方焦点的距离，符号规定同物距)；
• f’ ——象方焦距(从光心到象方焦点的距离，符号规定同物距)。
• f、f’ 的大小及透镜的几何形状(见图2—8，球面曲率半径一律以球面与光铀交点为计算起点量到球面曲率中心为止。从左向右为正，反之为负)、透镜材料的折射率n、透镜前后介质的折射率n。有关。薄透镜的焦距计算公式如下：

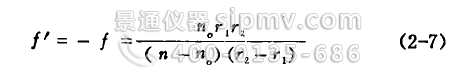
上式表示薄透镜放在同一介质中使用时，物方焦距和象方焦距的符号相反，绝对值相等。习惯上按象方焦距正负Θ，将透镜分为正透镜（f‘>0）和负透镜（f’<0）两类。对薄透镜而言，从公式（2-7）可以看出：n > n。 世凸透镜为正透镜；此时若把平行光入射于凸透镜，折射光线将向光轴靠拢，见图2-6b）；若把平行光射入于凹透镜，折射光将背离光轴散开，见图2-6d）。因此常称为正透镜为会聚透镜，负透镜为发散透镜。

利用公式（2-5）、（2-6）可以直接计算出物象之间的关系（位置、大小、正倒和虚实等），但也可以用作图法求出。作图法是根据光心和两焦点的性质选出从物点发出的如下三条典型光线：

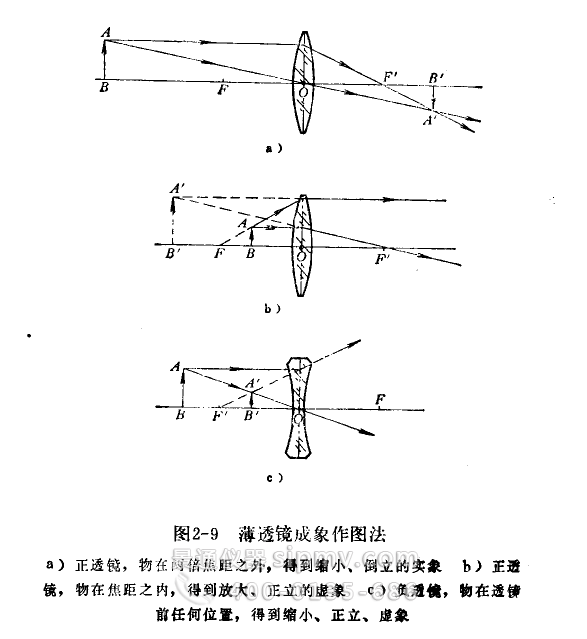
透镜放在同一种介质中使用时，通过光心的光线，一直穿过薄透镜不发生偏折；平行于光轴的入射光线，折射后通过象方焦点F'；通过物方焦点F的入射光线，折射后与光轴平行。然后画出物在透镜的两倍焦距之外所成的象【图2-9a）是一个倒立的缩小了的实像】；画出物在透镜焦距之内所戍的象[2—9b）是一个正立的放大了的虚象]；画出物在负透镜前的任何位置所得到的象【2—9c)是一个正立的缩小了的虚象】。这里值得指出的是，由了任何两条非平行光线总会有一交点，因此从上述三条典型光线中选出任何两条，使足够作图了。

注：Θ 是采取正向光路（入射光从左向右进行的光路）时，象方焦距的符号。